1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np

perch_length = np.array(
    [8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 
     21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 
     22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 
     27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 
     36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 
     40.0, 42.0, 43.0, 43.0, 43.5, 44.0]
     )
perch_weight = np.array(
    [5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 
     110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 
     130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 
     197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 
     514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 
     820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 
     1000.0, 1000.0]
     )

훈련 세트와 테스트 세트 분리

1
2
3
4
5
6
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
    perch_length, perch_weight, random_state = 42
)

train_input.shape, test_input.shape, train_target.shape, test_target.shape
((42,), (14,), (42,), (14,))

  • reshape(-1)은 무슨 의미인가?

    • x.reshape(-1)은 x.reshape(1, -1)과 같이 1차원 배열을 반환합니다.
    • x.reshape(-1, 1) => shape(12, 1)
    • x.reshape(-1, 2) => shape(6, 2)
    • x.reshape(-1, 3) => shape(4, 3)

    ++++ 출처: https://rfriend.tistory.com/345 [R, Python 분석과 프로그래밍의 친구 (by R Friend)]

1
2
3
4
train_input = train_input.reshape(-1, 1) # 행렬 재배치
test_input = test_input.reshape(-1, 1)

print(train_input.shape, test_input.shape)
(42, 1) (14, 1)

모델 만들기

1
2
3
4
5
6
7
from sklearn.neighbors import KNeighborsRegressor

# knn 클래스 부러오기
knr = KNeighborsRegressor(n_neighbors=3)

# 모형 학습
knr.fit(train_input, train_target)
KNeighborsRegressor(n_neighbors=3)

예측

  • p132
1
print(knr.predict([[50]]))
[1033.33333333]

시각화

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import matplotlib.pyplot as plt

# 50cm 농어의 이웃을 구하라
distances, indexes = knr.kneighbors([[50]])

# 훈련 세트의 산점도를 구하라

fig, ax = plt.subplots(figsize=(8, 5), facecolor="#c1f1f1")
plt.scatter(train_input, train_target)
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
plt.scatter(50, 1033, marker='^')
ax.set_xlabel('length')
ax.set_ylabel('weight')
plt.show()

png

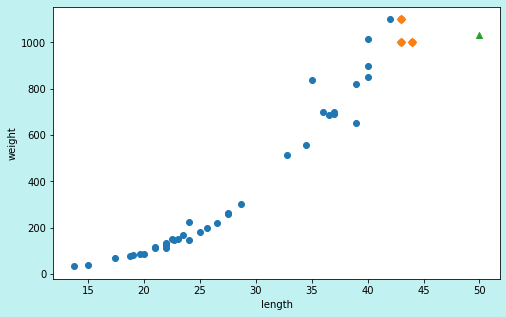
  • 머신러닝 모델은 주기적으로 훈련해야 합니다.
    • MLOps (Machine Learning & Operations)
    • 최근에 각광받는 데이터 관련 직업 필수 스킬!
    • 입사와 함꼐 공부시작 (데이터 분석가, 머신러닝 엔지니어, 데이터 싸이언티스트 희망자)

선형 회귀 (머신러닝)

  • 평가지표 확인이 더 중요! R2 점수, MAE, MSE
  • 5가지 가정들…
  • 잔차의 정규성
  • 등분산성, 다중공선성, etc..
  • 종속변수 ~ 독립변수간의 “인과관계”를 찾는 과정..
1
2
3
4
5
6
7
8
9
10
from matplotlib.ticker import LinearLocator
from sklearn.linear_model import LinearRegression

lr = LinearRegression()

# 선형 회귀 모델 훈련
lr.fit(train_input, train_target)

# 50cm 농어 예측
print(lr.predict([[200]]))
[7094.41034777]

1
2
3
4
5
6
7
fig, ax = plt.subplots(figsize=(8, 5), facecolor="#c1f1f1")
plt.scatter(train_input, train_target)
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
plt.scatter(50, 1033, marker='^') # 임의의 데이터 생성
ax.set_xlabel('length')
ax.set_ylabel('weight')
plt.show()

png

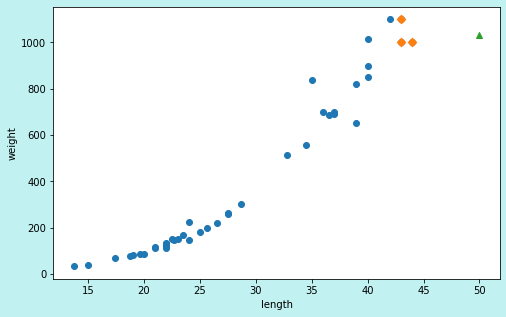
회귀식을 찾기

  • 하나의 직선을 그리려면 기울기와 절편이 있어야합니다.
  • 농어의 무게 = 기울기 x 농어 길이 + 절편
  • y = a * x + b
1
2
# 기울기, 상수
print(lr.coef_, lr.intercept_)
[39.01714496] -709.0186449535477
  • 기울기 : 계수 = 가중치(딥러닝, 기울기)
1
2
3
4
5
6
7
8
9
10
11
fig, ax = plt.subplots(figsize=(8, 5), facecolor="#c1f1f1")
plt.scatter(train_input, train_target)

# 15~50까지의 1차 방정식 그래프를 그린다.
plt.plot([15,50],
         [15 * lr.coef_ + lr.intercept_,
          50 * lr.coef_ + lr.intercept_])
ax.set_xlabel('length')
ax.set_ylabel('weight')
plt.scatter(50, 1241.8, marker='^')
plt.show()

png

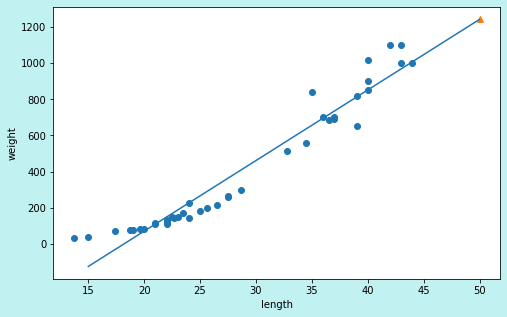
  • 모형 평가 (p.138)
    • 과소적합이 됨

다항회귀의 필요성

  • 치어를 생각해보자
  • 치어가 1cm
1
print(lr.predict([[1]]))
[-670.00149999]
  • (p. 140) 1차방정식을 2차방정식으로 만드는 과정이 나옴
  • 넘파이 브로드캐스팅 링크 텍스트
    • 배열의 크기가 동일하면 상관 없음
    • 배열의 크기가 다른데, 연산을 할때, 브로드캐스팅 원리가 적용
    • 브로드캐스팅 튜토리얼 등을 찾아서 추가적으로 공부를 해야함
1
2
3
4
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))

print(train_poly.shape, test_poly.shape)
(42, 2) (14, 2)

1
2
3
4
5
lr = LinearRegression()

lr.fit(train_poly, train_target)

print(lr.predict([[50 ** 2, 50]]))
[1573.98423528]

1
print(lr.coef_, lr.intercept_) # y = ax2 + bx + c 이차방적식, x = "length"
[  1.01433211 -21.55792498] 116.0502107827827
  • KNN의 문제점
    • 농어의 길이가 커져도 무게는 동일함 (현실성 제로)
  • 단순 선형회귀(1차 방정식)의 문제점
    • 치어(1cm)의 무게가 음수로 나옴 (현실성 제로)
  • 다항 회귀(2차 방정식)로 변경
    • 현실성 있음