|
Species |
Weight |
Length |
Diagonal |
Height |
Width |
| 0 |
Bream |
242.0 |
25.4 |
30.0 |
11.5200 |
4.0200 |
| 1 |
Bream |
290.0 |
26.3 |
31.2 |
12.4800 |
4.3056 |
| 2 |
Bream |
340.0 |
26.5 |
31.1 |
12.3778 |
4.6961 |
| 3 |
Bream |
363.0 |
29.0 |
33.5 |
12.7300 |
4.4555 |
| 4 |
Bream |
430.0 |
29.0 |
34.0 |
12.4440 |
5.1340 |
<script>
const buttonEl =
document.querySelector('#df-65932b7d-508a-47e0-8f70-ce7c6944b42c button.colab-df-convert');
buttonEl.style.display =
google.colab.kernel.accessAllowed ? 'block' : 'none';
async function convertToInteractive(key) {
const element = document.querySelector('#df-65932b7d-508a-47e0-8f70-ce7c6944b42c');
const dataTable =
await google.colab.kernel.invokeFunction('convertToInteractive',
[key], {});
if (!dataTable) return;
const docLinkHtml = 'Like what you see? Visit the ' +
'<a target="_blank" href=https://colab.research.google.com/notebooks/data_table.ipynb>data table notebook</a>'
+ ' to learn more about interactive tables.';
element.innerHTML = '';
dataTable['output_type'] = 'display_data';
await google.colab.output.renderOutput(dataTable, element);
const docLink = document.createElement('div');
docLink.innerHTML = docLinkHtml;
element.appendChild(docLink);
}
</script>
</div>
데이터 변환
1
2
3
| print(pd.unique(fish['Species']))
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
fish_input.shape
|
['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']
(159, 5)
- target 배열로 변환
- 종속변수
- to_numpy() method는 pandas 객체를 numpy 배열 객체인 ndarray로 반환 링크 텍스트
1
| fish_target = fish['Species'].to_numpy()
|
훈련 데이터와 테스트데이터
1
2
3
4
| from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
fish_input, fish_target, random_state = 42
)
|
표준화 전처리
- 데이터의 결측치 및 이상치를 확인하거나 제거하고 불일치되는 부분을 일관성 있는 데이터의 형태로 전환 하기도 하는 이 전 과정을 데이터의 전처리라고 일컫는다.
대표적인 사이킷런 스케일링의 종류
- StandardScaler : 기본 스케일. 평균과 표준편차 사용
- MinMaxScaler : 최대/최소값이 각각 1, 0이 되도록 스케일링
- MaxAbsScaler : 최대절대값과 0이 각각 1, 0이 되도록 스케일링
- RobustScaler : 중앙값(median)과 IQR(interquartile range) 사용. 아웃라이어의 영향을 최소화
1
2
3
4
5
6
| from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
|
1
2
3
| print(train_input[:5])
print(train_scaled[:5])
print(test_scaled[:5])
|
[[720. 35. 40.6 16.3618 6.09 ]
[500. 45. 48. 6.96 4.896 ]
[ 7.5 10.5 11.6 1.972 1.16 ]
[110. 22. 23.5 5.5225 3.995 ]
[140. 20.7 23.2 8.5376 3.2944]]
[[ 0.91965782 0.60943175 0.81041221 1.85194896 1.00075672]
[ 0.30041219 1.54653445 1.45316551 -0.46981663 0.27291745]
[-1.0858536 -1.68646987 -1.70848587 -1.70159849 -2.0044758 ]
[-0.79734143 -0.60880176 -0.67486907 -0.82480589 -0.27631471]
[-0.71289885 -0.73062511 -0.70092664 -0.0802298 -0.7033869 ]]
[[-0.88741352 -0.91804565 -1.03098914 -0.90464451 -0.80762518]
[-1.06924656 -1.50842035 -1.54345461 -1.58849582 -1.93803151]
[-0.54401367 0.35641402 0.30663259 -0.8135697 -0.65388895]
[-0.34698097 -0.23396068 -0.22320459 -0.11905019 -0.12233464]
[-0.68475132 -0.51509149 -0.58801052 -0.8998784 -0.50124996]]
k-최근접 이웃 분류기의 확률 예측
1
2
3
4
5
6
7
| from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier(n_neighbors=3)
kn.fit(train_scaled, train_target)
print(kn.score(train_scaled, train_target))
print(kn.score(test_scaled, test_target))
|
0.8907563025210085
0.85
182p
다중분류
- 타깃 데이터에 2개 이상의 클래스가 포함된 문제
1
2
3
4
| import numpy as np
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals = 4))
print(kn.classes_)
|
[[0. 0. 1. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 1. 0. ]
[0. 0. 0. 1. 0. 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]]
['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
로지스틱 회귀
중요도 : 최상
Why?
- 로지스틱 회귀
- 기초 통계로도 활용 (의학통계)
- 머신러닝 분류모형의 기초 모형인데, 성능이 생각보다 나쁘지 않음
- 딥러닝 : 초기모형에 해당됨.
로지스틱회귀(Logistic regression)와 선현 회귀(linear regression)의 차이점
- 선형회귀의 결과값은 연속적인값 , 오차값을 줄이기 위해 MSE(Mean Square Error)을 사용
- 로지스틱회귀의 결과값은 범주값, 그래프로 표현할시 0% ~ 100%로 사용하기 편함, 오차값을 줄이기 위해 Log Loss(cross entropy)를 사용
Youtube Link
이진 분류를 수행 할 때 시그모이드 함수의 출력이 0.5 보다 크면 양성 클래스, 0.5보다 작으면 음성 클래스로 판단(정확히 0.5일때 사이킷런은 음성 클래스로 판단.***라이브러리마다 다를 수 있음)
1
2
3
4
5
6
7
8
9
10
11
| import numpy as np
import matplotlib.pyplot as plt
z = np.arange(-5, 5, 0.1)
phi = 1 / (1 + np.exp(-z))
plt.plot(z, phi, color='green')
plt.xlabel('z')
plt.ylabel('phi')
plt.show()
|
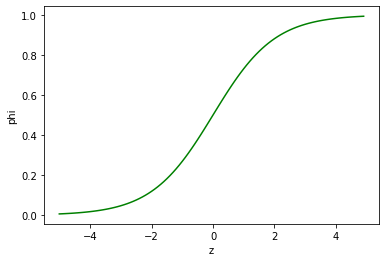
로지스틱 회귀로 이진 분류 수행하기
- 넘파이 배열은 True, False 값을 전달하여 행을 선택 할수 있음
1
2
| char_arr = np.array(['A', 'B', 'C', 'D', 'E'])
print(char_arr[[True, False, True, False, False]])
|
['A' 'C']
1
2
3
4
|
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
|
1
2
3
4
| from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
|
LogisticRegression()
1
2
3
4
|
print(lr.predict(train_bream_smelt[:5]))
|
['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
1
2
| print(lr.predict_proba(train_bream_smelt[:5]))
print(lr.classes_)
|
[[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]
['Bream' 'Smelt']
1
| print(lr.coef_, lr.intercept_)
|
[[-0.4037798 -0.57620209 -0.66280298 -1.01290277 -0.73168947]] [-2.16155132]
- z식
- z값을 출력하자!
- decisions_function() method 사용으로 z 값 구하기
1
2
| decisions = lr.decision_function(train_bream_smelt[:5])
print(decisions)
|
[-6.02927744 3.57123907 -5.26568906 -4.24321775 -6.0607117 ]
- scipy(사이파이) 라이브러리 안의 expit(시그모이드함수)() 사용
1
2
| from scipy.special import expit
print(expit(decisions))
|
[0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]
로지스틱 회귀로 다중 분류 수행하기
- LogisticRegression 클래스는 기본적으로 반복적인 알고리즘을 사용합니다. max_iter 매개변수에서 반복 횟수를 지정하며 기본값은 100입니다. 여기에 준비한 데이터셋을 사용해 모델을 훈련하면 반복 횟수가 부족하다는 경고가 발생합니다. 충분하게 훈련시키기 위해 반복 횟수를 1,000으로 늘리겠습니다.
- 기본적으로 릿지 회귀와 같이 계수의 제곱을 규제합니다. 이런 규제를 L2 규제라고도 부릅니다. 릿지 회귀에서는 alpha 매개변수로 규제의 양을 조절했습니다. alpha가 커지면 규제도 커집니다. LogisticRegression에서 규제를 제어하는 매개변수는 C입니다. 하지만 C는 alpha와 반대로 작을수록 규제가 커집니다. C의 기본값은 1입니다. 여기에서는 규제를 완화하기 위해 20으로 늘리겠습니다.
1
2
3
4
| lr = LogisticRegression(C = 20, max_iter = 1000)
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target))
print(lr.score(test_scaled, test_target))
|
0.9327731092436975
0.925
- 과대적합 및 과소적합으로 치우치지 않았기 때문에 처음 5개의 샘플에 대한 예측을 출력.
1
| print(lr.predict(test_scaled[:5]))
|
['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
1
2
| proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals = 3))
|
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
1
| print(lr.coef_.shape, lr.intercept_.shape)
|
(7, 5) (7,)
- 이진 분류에서는 시그모이드 함수를 사용해 z를 0과 1사이의 값으로 변환했습니다. 다중 분류는 이와 달리 소프트맥스(softmax) 함수를 사용하여 7개의 z값을 확률로 변환합니다.
- 소프트맥스 함수란 : 여러 개의 선형 방정식의 출력값을 0~1 사이로 압축하고 전체 합이 1이 되도록 만듭니다. 이를 위해 지수 함수를 사용하기 때문에 정규화된 지수 함수라고도 부릅니다.
- 소프트맥스 티스토리 링크
1
2
3
|
decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals = 2))
|
[[ -6.5 1.03 5.16 -2.73 3.34 0.33 -0.63]
[-10.86 1.93 4.77 -2.4 2.98 7.84 -4.26]
[ -4.34 -6.23 3.17 6.49 2.36 2.42 -3.87]
[ -0.68 0.45 2.65 -1.19 3.26 -5.75 1.26]
[ -6.4 -1.99 5.82 -0.11 3.5 -0.11 -0.71]]
1
2
3
4
|
from scipy.special import softmax
proba = softmax(decision, axis = 1)
print(np.round(proba, decimals = 3))
|
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]

